南山小马

南山小马

0%

动态规划

发表于 更新于 分类于 Disqus：

动态规划是一种算法设计技术，是一种使多阶段决策过程最优的通用方法。

如果问题是由交叠的子问题构成的，我们就可以用动态规划技术来解决它。一般来说这样的子问题出现在对给定问题求解的递推关系中，这个递推关系中包含了相同类型的更小问题的解。
动态规划法建议，与其对交叠的子问题一次又一次地求解，还不如对每个较小的子问题只求解一次并把结果记录在表中，这样就可以从表中得出原始问题的解。
动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再合并子问题的解以得出原问题的解。

币值最大化问题

问题：给定一排n个硬币，其面值均为整数c1, c2, …, cn, 这些整数并不一定两两不同。问如何选择硬币，使得在其原始位置互不相邻的条件下，所选硬币的总金额最大。

令：F(n)为最大可选金额，该题可分为两种情况，包括最后一枚硬币和不包括最后一枚硬币。第一种情况：可选硬币的最大金额为${c_n} + F\left( {n - 2} \right)$，即最后一枚硬币的面值加上之前的$n-2$枚硬币的可选最大金额。第二种情况，可选的最大金额为$F\left( {n - 1} \right)$，因此得到递推方程：

$$F\left( n \right) = \max \left\{ {{c_n} + F\left( {n - 2} \right),F\left( {n - 1} \right)} \right\},n > 1$$ $$F\left( 0 \right) = 0,F\left( 1 \right) = {c_1}$$

算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
private void maxCoinValue() {
    // 输入的值
    int[] coins = new int[]{5, 1, 2, 10, 6, 2};

    int[] f = new int[coins.length];
    f[0] = coins[0];
    f[1] = Math.max(coins[0], coins[1]);

    for (int i = 2; i < coins.length; i++) {
        f[i] = Math.max(f[i - 2] + coins[i], f[i]);
    }

    System.out.println(f[f.length - 1]);
}

找零问题

需找零金额为$n$，最少要用面值为${d_1} < {d_2} < \cdots < {d_m}$的硬币？

设F(n)为总金额为n的数量最小的硬币数目，为方便起见定义F(n)=0. 获得n的途径只能是：在总金额为$n - {d_j}$的一堆硬币上加入一个面值为${d_j}$的硬币，并且$n \geqslant {d_j}$。因此，我们只需要考虑所有满足上述要求的${d_j}$并选择使得$F(n - {d_j}) + 1$最小的${d_j}$即可。于是可得递归公式：

$$\left\{ \begin{gathered} F(n) = \mathop {\min }\limits_{j:n \geqslant {d_j}} \{ F(n - {d_j})\} + 1,n > 0 \hfill \\ F(0) = 0 \hfill \\ \end{gathered} \right.$$

算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
private void changeMaking() {
    // 输入数据
    int[] coins = new int[]{1, 3, 4};
    int n = 6;

    // f(n) 为总金额为n的数量最小的硬币数目
    int[] f = new int[n + 1];
    f[0] = 0;

    for (int i = 1; i <= n; i++) {
        int min = Integer.MAX_VALUE;
        int j = 0;
        while (j < coins.length && i >= coins[j]) {
            min = Math.min(f[i - coins[j]], min);
            j++;
        }
        f[i] = min + 1;
    }
    System.out.println(f[n]);
}

硬币收集问题

在n*m格木板中放有一些硬币，每格的硬币数目最多为一个，在木板左上方的一个机器人需要收集尽可能多的硬币并把它们带到右下方的单元格。每一步，机器人可以从当前的位置向右移动一格或向下移动一格。当机器人遇到一个有硬币的单元格时，就会将这枚硬币收集起来。设计一个算法找出机器人能找到的最大硬币数并给出相应的路径。
硬币收集问题1
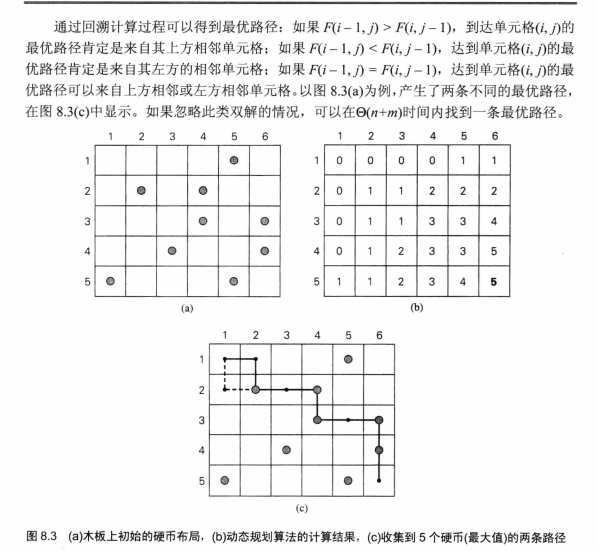
硬币收集问题2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
private void robotCoinCollection() {
    // 输入数据
    int[][] coins = new int[5][6];
    coins[0][4] = 1;
    coins[1][1] = 1;
    coins[1][3] = 1;
    coins[2][3] = 1;
    coins[2][5] = 1;
    coins[3][2] = 1;
    coins[3][5] = 1;
    coins[4][0] = 1;
    coins[4][4] = 1;

    // f(i,j) 为机器人截止到 i, j 单元格能够收集到的最大硬币数
    int[][] f = new int[coins.length][coins[0].length];
    f[0][0] = coins[0][0];

    for (int i = 1; i < coins[0].length; i++) {
        f[0][i] = f[0][i - 1] + coins[0][i];
    }

    for (int i = 1; i < coins.length; i++) {
        f[i][0] = f[i - 1][0] + coins[i][0];
        for (int j = 1; j < coins[0].length; j++) {
            f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]) + coins[i][j];
        }
    }

    System.out.println(f[coins.length - 1][coins[0].length - 1]);
}