先放上一道题:
有 A 和 B 两路公交车,平均发车间隔分别为 5 分钟和 10 分钟。某乘客在站点 S 可以 任意选择两者之一乘坐,假定 A 和 B 到达 S 的时刻无法确定,那么该乘客的平均等待时间约为____。
A、1 分钟 20 秒 B、3 分钟 20 秒 C、2 分钟 30 秒 D、1 分钟 40 秒
这是一道阿里校招题,同时在头条面试中也问了这道题。这一题有点复杂,咋们先看看其他概率题。
几何概型
如果每个事件发生的概率只与构成该事件区域的长度(面积或体积或度数)成比例,则称这样的概率模型为几何概率模型,简称为几何概型。
比如:对于一个随机试验,我们将每个基本事件理解为从某个特定的几何区域内随机地取一点,该区域中每一个点被取到的机会都一样;而一个随机事件的发生则理解为恰好取到上述区域内的某个指定区域中的点。这里的区域可以是线段,平面图形,立体图形等。用这种方法处理随机试验,称为几何概型.
简单来说,就是通过画图来求事件发生的概率:
取一根长度为30cm的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于10cm的概率有多大?
解、记事件M为“剪得两段的长度都不小于10cm,
那么事件M所在区域为线段AB,长度为10cm,
试验所取得所有结果所在的区域为整个绳长30cm。
那么,根据几何概型概率计算公式有:
$$p(M) = \frac1030 = \frac{1}{3}$$
假设张明家订了一份报纸,送报人可能在早上6:30—7:30之间把报纸送到家,他父亲离开家去工作的时间在早上7:00—8:00之间,问他父亲在离开家前能得到报纸(称为事件A)的概率是多少?
同理我们还是画图:
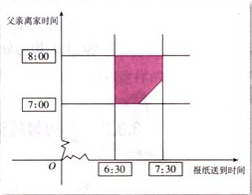
解:以横坐标x表示报纸送到时间,以纵坐标y表示张明父亲离家时间建立平面直角坐标系,假设随机试验落在方形区域内任何一点是等可能的,所以符合几何概型的条件.
根据题意,只要点落到阴影部分,就表示他父亲在离开家前能得到报纸,它的约束条件是$x < y$,即时间A发生,所以
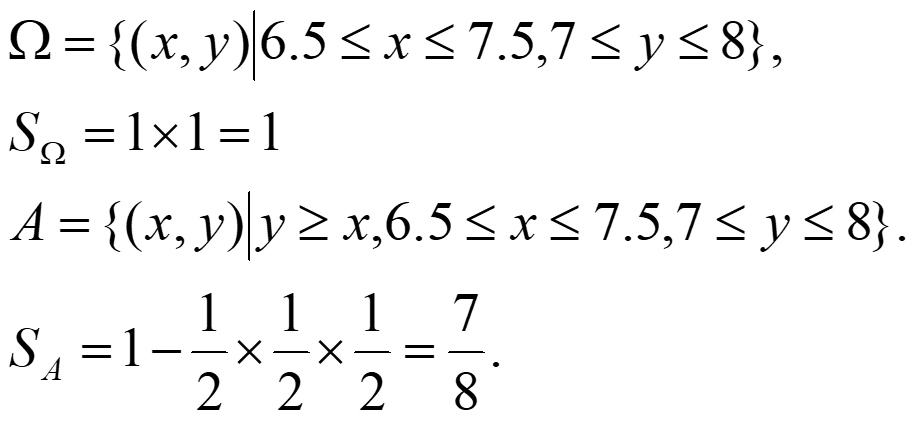
在一个周五晚上,甲和朋友乙决定去夜店High一把。但是他们兴奋过头,忘记了约定的具体时间,只记得是在十二点到一点之间。假设他们随机地选择到达夜店的时间,并且都会在店门口等另一个人十分钟(如果在此期间对方并未出现,他就会离开)。那么,他们当晚能见面的概率是多大呢?
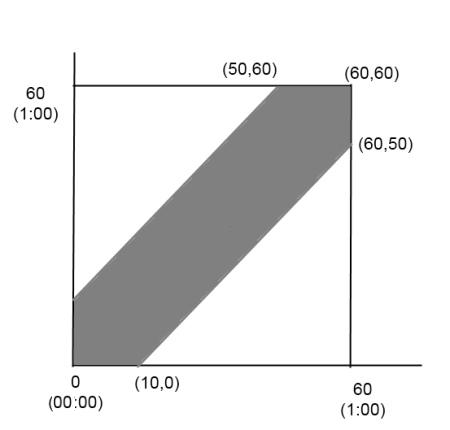
如果把甲的到达的时间记在 x 轴上,把乙的到达时间记在 y 轴上,那么他们到达的时间便可以用坐标系中的点 ( x , y ) 来表示,根据设定可知这个点一定会落在图中的正方形区域中。而如果二人想见面,那么他们先后到达的时间间隔一定要小于十分钟,即 | x – y | ≤ 10。
解这个不等式,可得 x – 10 ≤ y ≤ x + 10 。将这两条支线在坐标系中画出来,就能发现它们围成的区域正好是上图的阴影部分。
换言之,如果两人要碰面,对应的到达的时间点 (x,y) 就必须要落在阴影部分内。所以阴影部分的面积与大正方形面积之比就是所要求的概率,据此我们就能很轻松地计算出答案:11/36。
平均等公交时间
回到一开始的题目。
我们可以画一个图(至于图为什么是这样,我也没看明白,请大家参考阿里巴巴2014北京校招等车概率题分析
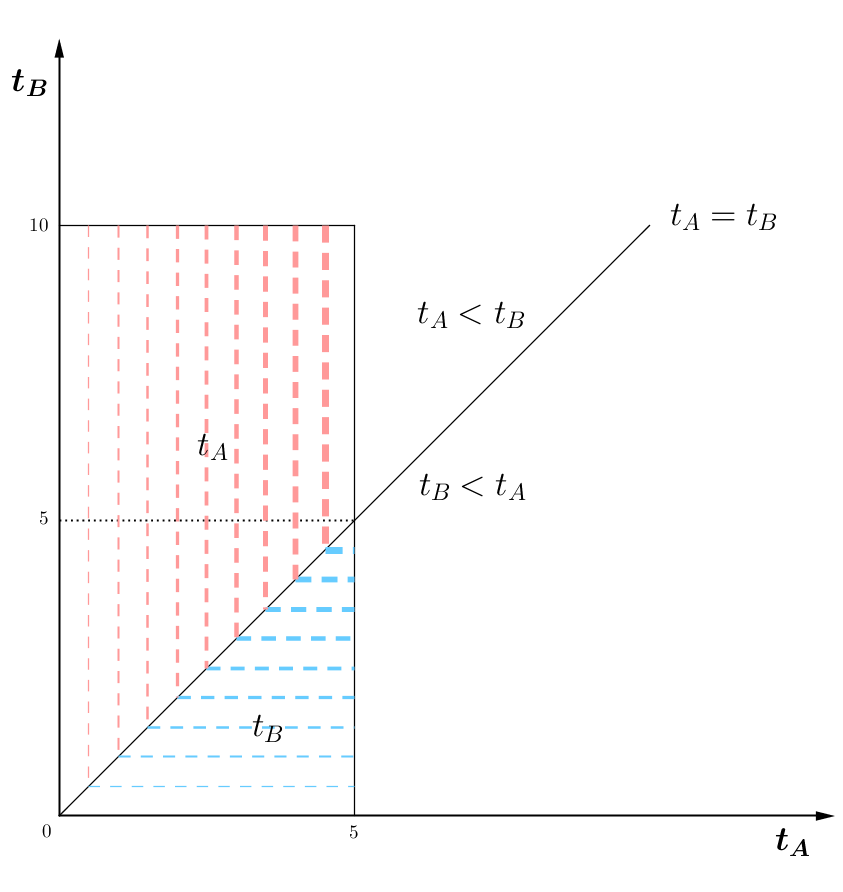
想象成一个长方体,切了两刀,图中的虚线可以理解为等高线,右边的高度为5 ($min({t_A},{t_B})$),左边为0,底边长为10,宽为5。
解法是 它的体积 / 它的底面积
$$E[t] = (125/2 + 125/3)/50 = 25/12$$
参考资料
几何概形ppt
阿里巴巴2014北京校招等车概率题分析
死理性派碰面法,100%遇见你
等公交车的概率:等待的时间比你想象的更久
上班有A和B两班公交,A车间隔为0-15分钟,B车间隔为0-20分钟(均随机),那么我上班平均等多久?
阿里题网页截图