Structural Deep Network Embedding

论文阅读Structural Deep Network Embedding
本文的PDF版深层网络结构嵌入
这学期选了非线性电路与系统，最近又在做网络表示的相关研究，特将平时看过比较好的论文写一写，和大家分享一下。

简介

信息网络在现实世界中普遍存在，例如航空公司网络，出版物网络，通信网络和万维网。这些信息网络的规模从几百个节点到数百万和数十亿个节点不等。大规模信息网络的分析在学术界和工业界引起越来越多的关注。本文研究的是将信息网络嵌入到低维空间的问题，其中每个顶点都表示为一个低维向量。这种低维嵌入在各种应用中非常有用，如可视化，节点分类，链路预测和选择推荐。

网络嵌入目前依旧面临许多挑战。（1）高维且非线性，深层的网络结构特征通常是非线性且高维的。因此，如何去描述学习这种高维非线性的特征是非常具有挑战性的。（2）结构保持，为了能够将结果应用到一些具体的网络分析任务中，网络嵌入方法需要能够将网络结构较好的保存下来，但是隐藏的网络结构是非常复杂并且难以发现的。节点的特性往往依赖于其局部和全局的网络结构。（3）稀疏性，真实世界中的大部分网络都是稀疏的，只能够利用极少数已发现的关系连接，因此还远远不能依此得到满意的效果。
近些年来，许多网络嵌入的方法相继被提出，它们采用了一些浅显的模型，比如说：IsoMAP，Laplacian Eigenmap(LE)，Line。由于这些模型的局限性，它们很难获得网络高维的非线性特征。为了解决这个难题，本文提出了深层模型来学习网络中的节点表示。我们受深度学习的启发，因为其展现出了强大的表示学习能力，能够从复杂的网络中学习特征。它已经在图像、文本、语音等方面取得了卓越的成绩。特别的，我们提出的模型设计了多层的网络结构，这些结构是由许多非线性函数构成，能够将网络数据映射到隐藏的非线性空间中，从而挖掘出网络的非线性结构。
为了处理网络结构保存以及稀疏性问题，我们把一阶相似度和二阶相似度相结合，并融于学习过程中。一阶相似度是两个顶点之间的局部点对的邻近度，但由于网络的稀疏性，许多真实存在的边可能缺失，因此，一阶相似度不足以表示网络结构。因此我们更进一步地提出了二阶相似度，一对顶点之间的接近程度表示在网络中其邻域网络结构之间的相似性。通过一阶相似度和二阶相似度，我们可以很好的捕获网络的局部特性与全局特性。为了保证网络的局部和全局特性在我们的模型中有较好的表示，我们提出了一种半监督的结构，其中，无监督部分重构了二阶相似度，以保持全局网络结构。而有监督的部分利用一阶相似度作为监督信息来保存网络的全局结构。因此，所学的表示能够很好的保存网络的局部和全局结构。此外，从图1可以看出，在许多网络中二阶相似度邻近点对的数目比一阶相似度多很多。由此可以得到，二阶相似度的引入能够在描述网络结构方面提供更多的信息。因此，我们的方法对稀疏网络是鲁棒的。

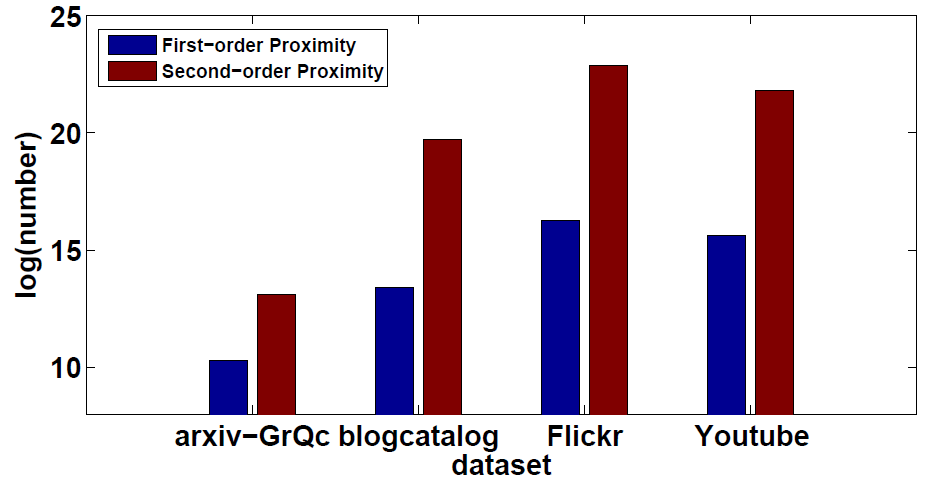
图1

主要贡献

我们提出了一种深层网络结构嵌入的方法，称为SDNE。这种方法能够将网络数据映射到深层的非线性低维空间，并且具有较好的鲁棒性。同时具我们所知，该方法是第一次将深度学习运用于网络表示中。
我们提出了一个新的半监督深层模型，整合了网络中的一阶和二阶相似性。因此，通过该模型得到的低维网络表示，能够很好的表现网络的局部和整体特征。
我们提出的算法在5个真实的数据集中，分别对2种应用问题（多标签分类、可视化）进行了实验验证。结果显示，对于网络标签稀少的数据，我们比其它基准方法提升了至少20%的效果。在某些情况下，我们只需要60%甚至更少的训练数据，也能得到很好的成绩。

其他相关工作

IsoMAP

算法主要步骤：

通过k-Nearest neighbor算法得到每个点的一个近邻。（参数k）
通过最短路算法构造一个N*N的距离矩阵。
通过Multi-dimensional Scaling算法根据距离矩阵进行非线性降维。（参数e）
算法结束以后，我们得到的就是一些e维空间的点。

DeepWalk

算法主要步骤：
在图上随机游走产生长度为$2w + 1$的路径，对每个点随机$\gamma $个随机游走序列。每一条随机游走路径便是相当于一个序列（相当于一句话），这样序列中的点就有上下文，定义一个时间窗口$w$，并进行马尔可夫假设，最后使用word2vec中的Skip-Gram训练每一个节点的向量。
Gram训练每一个节点的向量。
假设一个路径序列为$S = \left\{ {{v_1},...,{v_{|S|}}} \right\} $,对于${v_i} \in S$，其上下文为$C = \left\{ {{v_{i - w}},{v_{i - w + 1}},...,{v_{i + w - 1}},{v_{i + w}}} \right\}$, 那么DeepWalk的优化目标为:

$$f = \frac{1}{{\left| S \right|}}\sum\limits_{i = 1}^{\left| S \right|} {\sum\limits_{ - w \le j \le w,j \ne 0} {\log p({v_{i + j}}|{v_i})} } $$

其中：

$$p\left( {{v_j}|{v_i}} \right) = \frac{{exp\left( {c_{{v_j}}^T{r_{{v_i}}}} \right)}}{{\sum\nolimits_{v \in C} {exp\left( {c_{{v_j}}^T{r_{{v_i}}}} \right)} }}$$ ${r_{{v_i}}}$是点${v_i}$的向量表征, ${c_{{v_i}}}$是点${v_i}$上下文中点${v_j}$的向量表征。

DeepWalk使目标$f$最大化，使用Skip-Gram与Hierarchical Softmax进行训练得到每个点的vector，DeepWalk等价于MF(matrix factorization,矩阵分解)。

深层网络结构嵌入

定义1（网络）：给定一个网络$G = \left( {V,E} \right)$，其中$V = \{ {v_1}, \cdots ,{v_n}\} $表示为n个节点，$E = \{ {e_{i,j}}\} _{i,j = 1}^n$表示网络中所有边的集合。每一条边${e_{i,j}}$与其网络中边的权重${s_{i,j}} \ge 0$相关联。如果${v_i}$和${v_j}$之间没有连接，那么${s_{i,j}} = 0$，否则，对于无权图${s_{i,j}} = 1$，有权图${s_{i,j}} > 0$
网络嵌入的目的是将原始的高维网络数据映射到低维的表示空间中，网络中的每一个节点即可表示为一个低维向量，同时网络计算将会变得非常方便。正如我们之前提到的，网络的局部结构和全局结构都非常有必要在降维后保存下来，下面将详细定义一阶相似度和二阶相似度。
定义2（一阶相似度）：网络中的一阶相似度是两个顶点之间的局部点对的邻近度。对于由边（u，v）链接的每对顶点，该边的权重${s_{u,v}}$表示u和v之间的一阶相似性，如果在u和v之间没有边，它们的一阶相似度为0。
一阶相似度通常意味着现实世界网络中两个节点的相似性。例如，在社交网络中成为朋友的人往往具有类似的兴趣；在万维网上互相链接的页面往往谈论类似的主题。由于一阶相似度的重要性，许多现有的图嵌入算法，如IsoMap，LLE，Laplacian Eigenmaps目的都是保持一阶相似度。
然而，在现实世界的信息网络中，能够观察到的链接只是小部分，许多隐藏的其他关系都没有被观察到。缺失链路上的一对节点，即使它们在本质上非常相似，然而他们的一阶相似度为0。因此，只有一阶相似度对维持网络结构来说不是很有效。我们自然而然的想到，具有类似邻居的顶点往往是相似的。例如，在社交网络中，分享相同内容的人往往具有相似的兴趣，从而成为朋友，在文本网络中，总是与同一组词汇共同出现的词往往具有相似的含义。因此，我们定义二阶相似度，其补充了一阶相似性并能够保留网络结构。
定义3（二阶相似度）：二阶相似度对应于网络中的点对（u，v）是其邻域网络结构之间的相似性。数学上，让${{\rm{\mathcal{N}}}_u} = \{ {s_{u,1}}, \cdots ,{s_{u,\left| V \right|}}\} $表示一阶附近 u 与所有其他的顶点，那么 u 和v之间的二阶相似性由${{\rm{\mathcal{N}}}_u}$和${{\rm{\mathcal{N}}}_v}$之间的相似性来决定。如果没有一个顶点同时和 u 与 v 链接，那么 u 和 v的二阶相似性是0。
定义4（网络嵌入）：给定网络$G = \left( {V,E} \right)$，网络嵌入的问题是将每个顶点$v \in V$表示为低维空间${\mathbb{R}^d}$中的向量，学习函数$f:\left| V \right| \mapsto {\mathbb{R}^d}$，其中$d \ll \left| V \right|$。在空间${\mathbb{R}^d}$中，顶点之间的一阶相似度和二阶相似度都被保留。

SNDE模型

算法框架

在本篇文章中，我们提出了一个半监督的网络嵌入深度框架，整体框架如图2所示。具体来说，为了捕捉高维非线性的网络结构，我们提出了一个深层的体系结构，它由多个非线性映射函数组成，将输入数据映射到一个高维非线性的隐藏空间，以捕获网络结构。为了解决网络结构保持和稀疏性问题，我们提出了一个半监督模型来利用一阶和二阶相似度。对于每个顶点，我们都可以得到它的邻域。因此，我们设计了无监督的组件来保持二阶相似度，并重建每个顶点的邻域结构。同时，对节点的一部分，我们可以获得他们的一阶相似度。因此，我们设计了有监督的组件，利用一阶相似度作为监督信息来改进隐藏空间中的表示。通过联合优化所提出的半监督深度模型，SDNE可以保持高维的非线性网络结构，保证稀疏网络的健壮性。在接下来的部分中，我们将详细介绍如何实现半监督的深度模型。

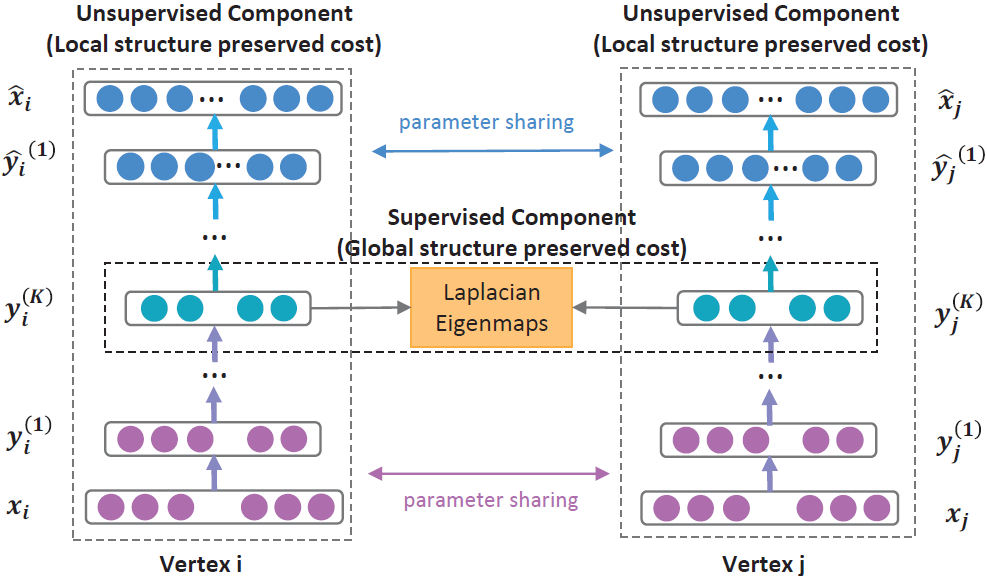
图2.网络整体结构

损失函数

我们首先描述无监督组件如何利用二阶近似保持全局网络结构。
二阶相似性值指的是节点的邻居相似，因此模型的二阶相似性，需要每个节点邻居的性质。给定一个网络$G = \left( {V,E} \right)$，我们可以获得到它的邻接矩阵S，它包含了n个元素${s_1}, \cdots {s_n}$，对于每一个元素${s_i} = \{ {s_{i,j}}\} _{j = 1}^n$，如果${v_i}$与${v_j}$间有相连的边，那么${s_{i,j}} > 0$。因此，${s_i}$描述了节点${v_i}$的邻居结构，$S$提供了每一个节点的邻居结构信息。对于$S$来说，我们将传统的深度自编码器的进行延伸，用来保存网络的二阶相似性。
下面简单回顾一下深度自编码器的主要思想。它属于一种非监督模型，包含编码器与解码器。编码器由许多非线性函数构成，将输入数据映射到表示空间。对应的，解码器也由许多非线性函数构成，它将表示空间映射到输入数据的重构空间。给定输入数据${x_i}$，其中对于各个层的隐藏表示如下公式进行计算：

$$y_i^{(1)} = \sigma ({W^{(1)}}{x_i} + {b^{(1)}})$$ $$y_i^{(k)} = \sigma ({W^{(k)}}y_i^{(k - 1)} + {b^{(k)}}),k = 2, \cdots ,K$$

通过一系列编码器的计算，我们可以获得输出${\hat x_i}$。自动编码器的目标是尽量减少输入和输出的重构误差。损失函数可以表示为：

$${\rm{\mathcal{L}}} = \sum\limits_{i = 1}^n {\left\| {{{\hat x}_i} - {x_i}} \right\|_2^2} $$

通过最小化损失函数能够较好的还原输入数据的原始表达，其表示空间能够提取出原始输入数据的特征。基于上述特性，我们将网络的邻接矩阵S作为自动编码器的输入，如： ${x_i} = {s_i}$，那么每一个元素${s_i}$表示节点${v_i}$邻居节点的特征。因此，通过重构可以让具有相似邻居结构的节点在隐藏的表示空间也具有相似的表达。但是，仅仅通过这种方式还不能直接解决问题。因为在网络中，我们可以观察到一些连接，但是也有一些合法的连接是缺失的。此外，由于网络的稀疏性，在邻接矩阵$S$中，零元素远远大于非零元素。如果我们直接将S输入到传统的自编码器中，可能会导致大量的零元素出现在重构空间，这并不是我们想要的结果。为了解决这个问题，我们让其对非零元素的重构误差比零元素的惩罚更大。改进的目标函数如下所示：

$$\begin{array}{l}{{\rm{\mathcal{L}}}_{2nd}} = \sum\limits_{i = 1}^n {\left\| {({{\hat x}_i} - {x_i}) \odot {b_i}} \right\|_2^2} \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left\| {(\hat X - X) \odot B} \right\|_F^2\end{array}$$

其中$ \odot $表示Hadamard积，${b_i} = \{ {b_{i,j}}\} _{j = 1}^n$，如果${s_{i,j}} = 0$，那么${b_{i,j}} = 1$，否则${b_{i,j}} = \beta > 1$。通过这种改进的损失函数，可以更好的让具有相似邻居的点在获得的表示空间也相似。换句话说，这个非监督部分能够很好的保存网络的二阶相似度。
不仅要维持全局网络结构，而且要捕获局部结构。我们使用一阶相似度表示网络局部结构。一阶相似度可以作为监督信息来约束一对顶点在隐藏表示空间的相似性。因此，我们设计了监督部分来利用一阶相似度。损失函数如下所示：

$$\begin{array}{l}{{\rm{\mathcal{L}}}_{1nd}} = \sum\limits_{i = 1}^n {{s_{i,j}}\left\| {y_i^{(K)} - y_j^{(K)}} \right\|_2^2} \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum\limits_{i = 1}^n {{s_{i,j}}\left\| {{y_i} - {y_j}} \right\|_2^2} \end{array}$$

其中${Y^{(k)}} = \{ y_i^{(k)}\} _{i = 1}^n$为编码器获得的隐藏表示空间。
该公式的灵感来源于拉普拉斯特征映射(Laplacian Eigenmaps)，在表示空间中，如果相似的节点相距较远，那么会受到一个较大的惩罚。通过这一操作，我们的模型能够很好的保持网络的一阶相似度。
我们同时考虑网络的一阶相似度和二阶相似度，另外在加上L2正则项，共同构成了自动编码器的损失函数：

$$\begin{array}{l}{{\rm{\mathcal{L}}}_{mix}} = {{\rm{\mathcal{L}}}_{2nd}} + \alpha {{\rm{\mathcal{L}}}_{1nd}} + \upsilon {{\rm{\mathcal{L}}}_{reg}}\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left\| {(\hat X - X) \odot B} \right\|_F^2 + \alpha \sum\limits_{i = 1}^n {{s_{i,j}}\left\| {{y_i} - {y_j}} \right\|_2^2} + \upsilon {{\rm{\mathcal{L}}}_{reg}}\end{array}$$

其中：

实验

数据集

为了能够全面地评价算法得到的低维表示，我们使用了5个真实的网络数据，包括3个社交网络，1个引文网络，1个语言网络；实验了2类网络应用任务，包括多标签分类和可视化。考虑到各个网络数据的本身属性，对于每一类应用，我们使用了至少一个数据集进行试验。数据集的参数如下表所示：

数据集	#(V)	#(E)
BLOGCATALOG	10312	667966
FLICKR	80513	11799764
YOUTUBE	1138499	5980886
ARXIV GR-QC	5242	28980
20-NEWSGROUP	1720	Full-connected

表1. 网络数据集参数

对比算法

我们实验与以下几个基准算法进行比较：DeepWalk、LINE、GraRep、Laplacian Eigenmaps、Common Neighbor。

评价指标

对于多标签分类问题，我们采用micro-F1和macro-F1指标进行评价。对于标签A，我们将TP（A），FP（A）和FN（A）分别表示为属于A的样本被正确分类到A的数目，不属于A的样本被错误分类到A的数目和不属于A的样本被正确分类到了类别A的其他类的数目。假设是整个标签集。Micro-F1和Macro-F1定义如下： Macro-F1是一个每个类的权重的度量。定义如下：

$$Macro - F1 = \frac{{\sum\nolimits_{A \in {\rm{\mathcal{C}}}} {F1(A)} }}{{\left| {\rm{\mathcal{C}}} \right|}}$$

其中F1(A)是标签A的F1度量。
Micro-F1是对每个实例权重的度量。定义如下：

$$\Pr = \frac{{\sum\nolimits_{A \in {\rm{\mathcal{C}}}} {TP(A)} }}{{\sum\nolimits_{A \in {\rm{\mathcal{C}}}} {(TP(A) + FP(A))} }}$$ $$R = \frac{{\sum\nolimits_{A \in {\rm{\mathcal{C}}}} {TP(A)} }}{{\sum\nolimits_{A \in {\rm{\mathcal{C}}}} {(TP(A) + FN(A))} }}$$ $$Micro - F1 = \frac{{2*\Pr *R}}{{\Pr + R}}$$

参数设置

我们在本文中提出了一种多层的神经网络结构，层数随不同的数据集而做相应调整。每层的神经元数目如表2所示。其中BLOGCATALOG，ARXIV GR-QC和20-EWSGROUP使用了三层神经网络，FLICKR和YOUTUBE使用了四层。如果我们使用更深的模型，性能几乎保持不变，甚至变得更糟。

数据集	每一层神经元数
BLOGCATALOG	10300-1000-100
FLICKR	80513-5000-1000-100
YOUTUBE	22693-5000-1000-100
ARXIV GR-QC	5242-500-100
20-NEWSGROUP	1720-200-100

表2. 神经网络结构
对于我们的方法，通过在验证集上使用网格搜索(grid search)来调整，和三个超参数。对于LINE，随机梯度下降的mini-batch大小设置为1。学习速率的初始值为0.025。负采样数(number of negative samples)为5，总采样数(the total number of samples)设为100亿。对于DeepWalk，我们将窗口大小设置为10，步长为40，每次采样40个顶点。对于GraRep，我们将最大转移矩阵步长(maximum matrix transition step)设置为5。

实验结果

多标签分类

我们通过本实验中的多标签分类任务来评估不同网络表示的有效性。顶点的表示是从网络嵌入方法生成的，并被用作将每个顶点分成一组标签的特征。具体来说，我们采用LIBLINEAR软件包来训练分类器。训练分类器时，我们随机抽取标签节点的一部分作为训练数据，其余作为测试。对于BLOGCATALOG，我们随机抽取10％至90％的顶点作为训练样本，并使用剩余顶点来测试性能。对于FLICKR和YOUTUBE，我们随机抽取1％至10％的顶点作为训练样本，并使用剩余顶点来测试性能。另外，我们删除没有在YOUTUBE中被任何类别标记的顶点。我们重复进行5次实验，取Micro-F1和Macro-F1指标的平均值进行度量。结果分别如图3到图5所示。

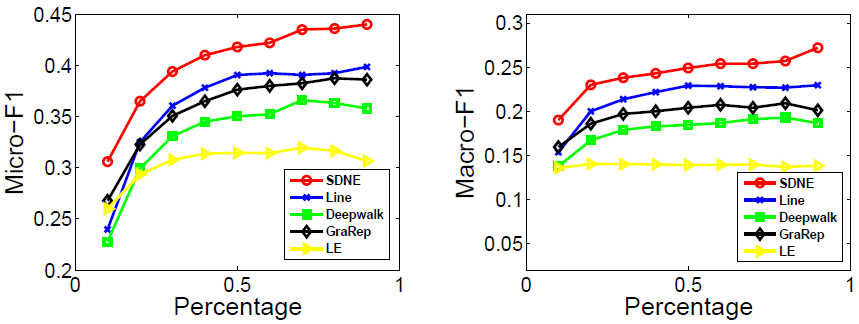
图3 .Micro-F1和Macro-F1在BLOGCATALOG上的表现

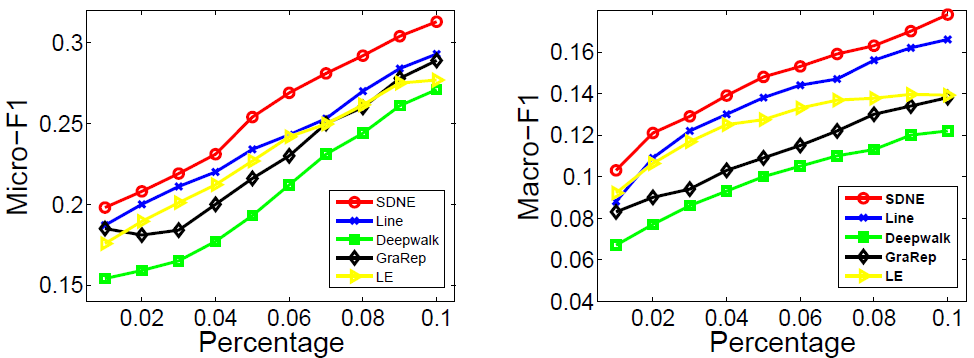
图4 .Micro-F1和Macro-F1在FLICKR上的表现

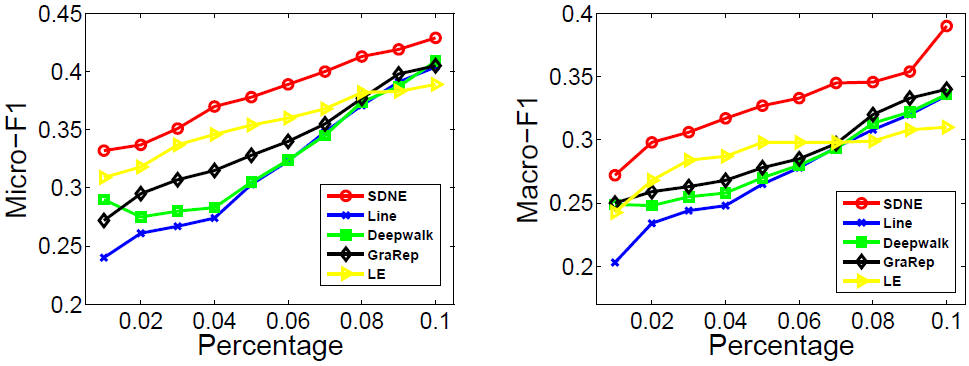
图5 .Micro-F1和Macro-F1在YOUTUBE上的表现
在图3到图5中，我们算法的曲线一直高于其他基准算法的曲线。它表明，在多标签分类任务中我们算法学习得到的网络表示比其他算法得到的效果更好。
在图3（BLOGCATALOG）中，当训练百分比从60％下降到10％时，我们的方法在基准线上的改善幅度更为明显。它表明当标签数据有限时，我们的方法可以比基准算法有更显着的改进。这样的优势对于现实世界的应用尤其重要，因为标记的数据通常很少。
在大多数情况下，DeepWalk的性能是网络嵌入方法中最差的。原因有两个方面。首先，DeepWalk没有明确的目标函数来捕获网络结构。其次，DeepWalk使用随机游走来获得顶点的邻居，由于随机性而引起了很多噪音，特别是对于度数高的顶点。

可视化

网络嵌入的另一个重要应用是在二维空间上生成网络的可视化。对此我们在20-NEWSGROUP网络进行可视化的实验。我们使用不同网络嵌入方法学习的低维网络表示作为可视化工具t-SNE的输入。因此，每个新闻组文档被映射为二维向量。然后我们可以将每个向量可视化为二维空间上的一个点。对于被标记为不同类别的文档，我们在对应的点上使用不同的颜色。因此，良好的可视化结果能让相同颜色的点彼此靠近。可视化结果如图6所示。

图6. 20-NEWSGROUP的可视化
每个点表示一个文档。点的颜色表示文档的类别。蓝色表示rec.sport.baseball的主题，红色表示comp.graphics的主题，绿色表示talk.politics.guns的主题。
从图7可以看出，LE和DeepWalk的结果并不理想，属于不同类别的点相互混合。对于LINE，形成不同类别的群集。然而，在中心部分，不同类别的文件仍然相互混合。对于GraRep，结果看起来更好，因为相同颜色的点分割成分组，但是，每个群体的边界不是很清楚。显然，SDNE的可视化效果在群体分离和边界方面都表现最好。

总结

在本文中，我们提出了一种深层网络结构嵌入，即SDNE来执行网络嵌入。具体来说，为了捕获高维非线性的网络结构，我们设计了一个具有多层非线性函数的半监督深度模型。为了进一步解决网络结构保持和稀疏问题，我们同时使用了一阶邻近度和二阶邻近度来表示网络的局部和全局特征。通过在半监督的深度模型中优化它们，所学习的表示能够体现出网络的局部和全局特征，并且对稀疏网络是鲁棒的。我们在真实的网络数据集上试验了多标签分类和可视化任务。结果表明，我们的算法与当前最好的算法(state-of-the-art)相比有本质性的提高。