简介
复杂网络聚类
各种各样的网络如合作者网络、万维网、神经网络，都可以被建模成复杂网络。网络聚类的任务就是将复杂网络划分成不同部分，这些部分我们把它称作社区。在非符号网络中，同一个社区内的节点比较稠密且互相紧密连接，在不同社区间的节点则连接较少。对于符号网络而言，无论是社区内部还是社区之间他们的连接都非常紧密。网络聚类有助于我们发现网络的组织结构和其功能。近些年来，大量的网络聚类方法被提出。
网络聚类可以被建模成优化问题，这里问题大部分都属于NP难问题。正因为这个原因，进化算法常用来解决这个问题，比如说GA-net，Meme-net。在某些应用中，我们同时考虑一些相互矛盾的因素，因此把它当成多目标优化问题，比如说MOGA-net，MOCD，MOEA/D-net。
多目标进化算法及粒子群算法
多目标进化算法(MOEAs)的目标是从多目标优化问题中的到一组帕累托最优解集(Pareto optimal solutions)，目前MOEAs可以大致分为三类，第一类是基于帕累托占优(Pareto dominance)比较著名的算法有NSGA-Ⅱ，SPEA2，PAES,AMOSA,第二类是基于绩效指标，第三类是基于分解，这些多目标优化的分解算法(MOP)转化为一系列单目标的子问题或者一些简单的多目标子问题，我们采用群体搜索的方法来解决这些子问题。
粒子群优化算法(PSO),最初是解决单目标优化方法的，详细介绍可参考我之前的文章【计算智能】目标优化智能算法之粒子群算法。
本文的贡献
- 根据复杂网络聚类问题，和传统的粒子群算法框架，我们重新定义了粒子的位置及速度更新策略。同时我们还重新定义了他们的运算操作，还介绍了特定问题的粒子群的初始化方法以及它们的扰动策略。
- 第一次将多目标优化问题的离散粒子群方法(MODPSO)应用到复杂网络聚类问题中。
- 提出了新的目标函数，通过大量的实验证实了该方法用于符号网络及非符号网络的有效性。
问题描述及动机
网络社区定义
一个网络中同时具有积极连接和消极连接被称为 符号网络(signed network) ， 非符号网络(unsigned network) 可以看成一个特殊的符号网络，它们只有积极连接。
定义一个非符号网络G=(V,E)，其中V表示节点，E表示边。特别的${k_i}$表示节点i的度，${A_{ij} = 1}$表示节点i和j直接连接，反之${A_{ij} = 0}$。给定$S \subset G$，其中节点i属于其中，$k_i^{in} = \sum\nolimits_{i,j \in S} {{A_{ij}}} $,$k_i^{out} = \sum\nolimits_{i,j \notin S} {{A_{ij}}} $使得${A_{ij}}$为内在的或者外在的节点的度，如果S为强感知(strong sense)，则有$$\forall i \in S,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k_i^{in} > k_i^{out}$$，如果S为弱感知(weak sense)，则$$\sum\limits_{i \in S} {k_i^{in}} > \sum\limits_{i \in S} {k_i^{out}} $$
对于符号网络，G=(V,PE,NE)，PE和NE分别为积极连接和消极连接。令A为权重邻接矩阵， ${A_{ij} = 1}$,if ${e_{ij}} \in PE$；${A_{ij} = -1}$,if ${e_{ij}} \in NE$；${A_{ij} = 0}$,if$\nexists {e_{ij}}$。给定$S \subset G$，其中节点i属于其中${(k_i^ + )^{in}} = \sum\nolimits_{j \in S,{e_{ij}} \in PE} {\left| {{A_{ij}}} \right|} $和${(k_i^ - )^{in}} = \sum\nolimits_{j \in S,{e_{ij}} \in NE} {\left| {{A_{ij}}} \right|} $分别为积极和消极的内在节点i的度数，特别的S为强感知如果满足
另外
由此可以看出，在强感知的情况下，在社区中一个节点拥有比消极连接更多的积极连接。在弱感知的情况下，在一个社区中积极连接非常稠密，同时在不同的社区直接它们的消极连接也非常稠密。
网络聚类问题
网络聚类问题可以被描述为一个优化问题，Girvan 和 Newman 提出了模块度函数（Q函数）$$Q = \frac{1}{{2m}}\sum\limits_{i,j} {({A_{ij}} - {k_i}{k_j}/2m)\delta (i,j)} $$其中m表示边数，${A_{ij}}$表示网络的邻接矩阵中的元素，${k_i}$表示节点i的度数，$\delta (i,j) = 1$表示节点i和节点j属于同一个社区，否则其为0。
Q函数适用于非符号网络，对于符号网络G´omez提出了SQ函数
其中${\omega _{ij}}$为邻接矩阵的权重，$\omega _i^ + (\omega _i^ - )$表示所有的积极（消极）权重之和。
但是Fortunato 和 Barthlemy指出模块度函数的局限性，而且符号网络的模型也同样存在。
……
在先前的工作中，对于非符号网络，我们将其看成一个多目标优化问题，其包括两个目标函数NRA和RC让他们达到最小，同时解决了模块度函数的限制。给定一个非符号网络G=(V,E)，|V|=n 节点数，|E|=m边数，A为邻接矩阵。令k为划分社区的个数,Ω={c1,c2,c3,…,ck}，${V_1},{V_2} \in \Omega $，我们定义$L({V_1},{V_2}) = \sum\nolimits_{i \in {V_1},j \in {V_2}} {{A_{ij}}}$
,$L({V_1},\overline {{V_2}} ) = \sum\nolimits_{i \in {V_1},j \in \overline {{V_2}} } {{A_{ij}}}$，其中$\overline = \Omega - {V_2}$，优化问题可以被定义为$$\min = \left\{ \begin{array}{l}NRA = - \sum\nolimits_{i = 1}^k {\frac{{L({V_i},{V_i})}}{{\left| {{V_i}} \right|}}} \\RC = \sum\nolimits_{i = 1}^k {\frac{{L({V_i},\overline {{V_i}} )}}{{\left| {{V_i}} \right|}}} \end{array} \right.$$
在本篇文章中，我们将NRA替换成了kernel k-means(KKM)，对于非符号网络聚类问题可以描述为$$\min = \left\{ \begin{array}{l}KKM = 2(n - k) - \sum\nolimits_{i = 1}^k {\frac{{L({V_i},{V_i})}}{{\left| {{V_i}} \right|}}} \\RC = \sum\nolimits_{i = 1}^k {\frac{{L({V_i},\overline {{V_i}} )}}{{\left| {{V_i}} \right|}}} \end{array} \right.$$
对于符号网络聚类问题，有一些区别，我们对KKM和RC做了一些简单的修改
其中${L^ + }({V_i},{V_j}) = \sum\nolimits_{i \in {V_i},j \in Vj} {{A_{ij}}} $,${A_{ij}} > 0$
${L^ - }({V_i},{V_j}) = \sum\nolimits_{i \in {V_i},j \in Vj} {\left| {{A_{ij}}} \right|} $,${A_{ij}} < 0$我们的动机
……
算法框架
粒子状态定义
为了更好的解决复杂网络聚类问题，在本文中，我们重新定义了PSO算法在离散中的情况。
-
位置
对某个粒子i，${X_i} = \{ {x_1},{x_2}, \cdots ,{x_n}\} $。粒子位置的每一个维度是从1到n的随机数，例：${x_i} \in [1,n]$，其中n为网络中所有节点的个数，如果${x_i} = {x_j}$那么我们认为节点i和j属于同一个集合
-
速度
粒子状态更新
在我们提出的DPSO框架中，速度决定了粒子移动的方向与距离。在速度更新之后，粒子将会使用该速度来更新自己的位置。在该问题中，无论是速度还是位置都是整形向量，传统的粒子更新策略将不再适用。因此我们重新定义了适合网络聚类问题的更新策略。首先我们重新定义粒子的速度更新策略
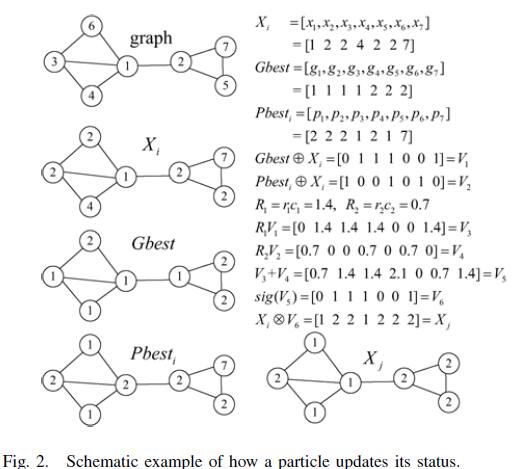
$${V_i} = sig(\omega {V_i} + {c_1}{r_1}({X_i} \oplus Pbes{t_i}) + {c_2}{r_2}({X_i} \oplus Gbest))$$式（10）
其中，ω为惯性权重，c1、c2是非负的常数，称为学习因子，r1、r1是分布于[0,1]的随机数。
$\oplus$为异或操作，Y=sig(X)，其中Y=(y1 ,y2 , … , yn), X=(x1 ,x2 , … , xn)被定义为：
其中sigmoid函数为：
$$sigmoid(x) = \frac{1}{{1 + {e^{ - x}}}}$$在该算法中，ω随机产生[0,1]，c1和c2设置为经典值1.494
基于刚刚新定义的粒子速度更新策略，我们重新定义粒子的位置更新策略
$${x_i}^t = {x_i}^t \otimes {v_i}^t$$ 式（13）
$\otimes$在粒子状态更新中是一个关键操作。它直接影响了粒子的飞行方向，一个良好的$\otimes$操作可以引导粒子飞向好的位置，避开差的状态。
给定一个位置${X_1} = \{ {x_{11}},{x_{12}},...,{x_{1k}}\} $和速度$V = \{ {v_1},{v_2},...,{v_n}\}$，位置$\otimes$速度得到一个新的状态，例：${X_1} \otimes V = {X_2}$,${X_2} = \{ {x_{21}},{x_{22}},...,{x_{2n}}\} $，其中${X_2}$被定义为：
其中$Nbes{t_i}$是一个整数，假设节点i的邻居为$N = { {n_1},{n_2}, \cdots ,{n_k}}$，$Nbes{t_i}$可由以下公式得出
$$Nbes{t_i} = \arg {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {\max }\limits_r \sum\limits_{j \in N} {\varphi ({x_{1j}},r)}$$
其中如果i = j，则$\varphi (i,j) = 1$，否则为0，函数$\arg {\max _r}f(x)$返回当f(x)取得最大值时的r。可以看出$Nbes{t_i}$为节点i的邻居节点集合的主要标签。这可以在现实生活中很好的理解，因为对于一个人而言，他更愿意加入他朋友最多的社区中。
在图二中，$X_i$和$Nbes{t_i}$是粒子i的当前位置和个体极值。Gbest是粒子群的群体最优。$V_1$，$V_2$，$V_3$，$V_4$，$V_5$，是中间变量。$V_6$和$X_j$，由式（10）和式（13）计算得到。
根据上述介绍，我们可以看出，我们提出的DPSO框架具有以下几个特性
- 粒子的位置和速度更新策略非常简单
- 新定义的操作非常容易实现，能够减少计算复杂度
- DPSO框架不需要事先了解网络结构，能够自动进行决策
粒子初始化
一个优秀的初始化方法能够减少搜索空间来减少算法达到最优解的时间同时还可以保证解的多样性。传统的随机生成初始化的方法会导致大量的冗余。在本篇文中，我们采用了先前工作中提出的 lable propagation-based initialization方法
假定节点i的邻居节点集为$\Omega (i) = ({x_1},{x_2}, \cdots ,{x_k})$，用l(i)来表示节点i属于的社区标记，首先我们将各个节点分别设置为各不相同的标记，如：l(i)=i，接下来每一个节点的社区标记依赖它的邻居节点，我们让它们的节点标记通过网络进行传播。我们假设网络中的每个节点选择加入其邻居的最大数量所属的社区。
其中如果i = j，则$\delta (i,j) = 1$，否则为0。我们迭代地执行这个过程，其中在每个步骤，每个节点基于其邻居的标签来更新其标签。 当传播迭代达到五个，并且如果我们将所有的团体标签形成为染色体，则所创建的候选个体具有高聚类精度，此外，我们可以获得相当多样的种群 。
算法的伪代码如下：
领袖选择
在本文中采用随机的策略来选择gbest，因为它既能够带来种群的多样性，又能够减少时间复杂度。对于一个粒子，有ns个相应的邻居（基于聚合权重系数向量之间的欧几里德距离定义）;然后我们从邻居中随机选择一个粒子作为领袖。
算法框架
在所提出的算法中，所采用的分解方法是广泛使用的契比雪夫Tchebycheff方法。
$${g^{te}}(x|\omega ,{z^*}) = \mathop {\max }\limits_{1 \le i \le k} {\kern 1pt} {\omega _i}\left| {{f_i}(x) - z_i^*} \right|$$$$subject{\kern 1pt} {\kern 1pt} to{\kern 1pt} {\kern 1pt} x \in \Omega $$
其中${z^*} = (z_1^*,z_2^*,z_3^*, \cdots ,z_k^*)$为参考点，$z_i^* = \{ \min {\kern 1pt} {f_i}(x)|x \in \Omega \} $,i=1,…,k
这个算法框架在上图中给出，其中第3.8步，通过使用帕累托占优的概念来更新pbest，即，如果新生成的解支配pbest解，则用新解来更新它; 如果pbest支配新产生的解，pbest保持其原始状态; 如果它们是相互非支配的，那么我们使用聚合方法来确定是否更新pbest。下面我们给出其算法2
震荡操作(Turbulence Operator)
为了保持多样性并帮助MOPSO逃离局部最优，许多现有的MOPSO采用震荡算子。 对于网络聚类问题，在我们的算法中，采用的震荡算子称为基于邻域的突变（NBM）。 该过程可以描述如下。首先，我们生成在0和1之间的伪随机数; 对于每个染色体中的每个基因，如果随机数小于突变概率pm，则将NBM过程应用于基因，即，将其标签标识符分配给其所有邻居。算法3
复杂性分析
……
实验分析
比较算法
MODPS, MOPSO-r1, MOPSO-r2, GA-net, Meme-net, MOGA-net, MOCD, MODA/D-net, GN, CNM, Informap
实验设置
对于已知网络的真实情况，我们采用归一化互信息（NMI）指数来估计真实聚类结果与检测到的聚类结果之间的相似性。 给定网络的两个分区A和B，令C是混淆矩阵，其元素$C_{ij}$是分区A中的社区i和分区B中的社区j共同共享的节点的数目。
$$NMI = \frac{{ - 2\sum\nolimits_{i = 1}^{{C_A}} {\sum\nolimits_{j = 1}^{{C_B}} {{C_{ij}}\log ({C_{ij}}N/{C_{i.}}{C_{.j}})} } }}{{\sum\nolimits_{i = 1}^{{C_A}} {{C_{i.}}\log ({C_{i.}}/N) + \sum\nolimits_{j = 1}^{{C_B}} {{C_{.j}}\log ({C_{.j}}/N)} } }}$$其中${C_A}({C_B})$是分区A(B)中的聚类数目。${C_{i.}}({C_{.j}})$是C中第i行（j列）的元素个数之和，N是网络中节点数，如果A=B则，NMI(A,B)=1,如果A,B完全不同则NMI(A,B)=0