这篇文章介绍 M. Gong, Q. Cai, L. Ma, and L. Jiao, “Big Network Analytics Based on Nonconvex Optimization,” 2016, pp. 345–373. 论文中的思想。由于刚开始学习,如有错误还请大家多多指正!也希望能和大家多多交流!
大数据问题可以被看做是一个网络问题。大部分的网络问题可以被建模成非凸优化问题,因此可以采用最优化的方式来解决,其中进化计算是一个有效的解决办法。在本篇文章中,我们着重介绍采用基于非凸优化方法的进化计算来解决社区检测问题。基于单目标和多目标在社区检测的优化问题我们接下来都会进行一个详细分析。一些基于经验且有效的网络分析优化方法也会进行介绍。
网络问题、特性、符号
近些年来,我们发现大数据是一个非常热门的话题。图一表示了网络与网络数据挖掘对网络分析的重要性。网络分析不仅仅能够找出隐藏在网络中的信息还能发现网络中某些重要的属性来控制网络的发展。在图二中,我们列举了12个网络分析中的关键问题。
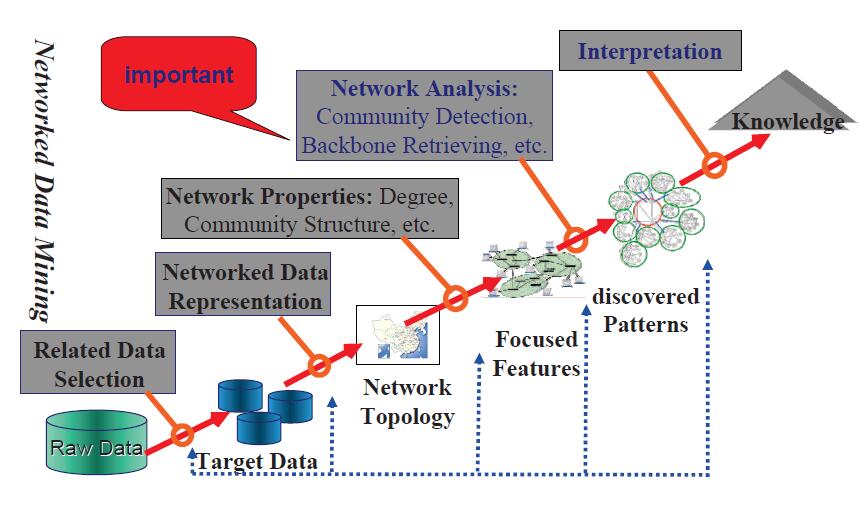 图一
图一
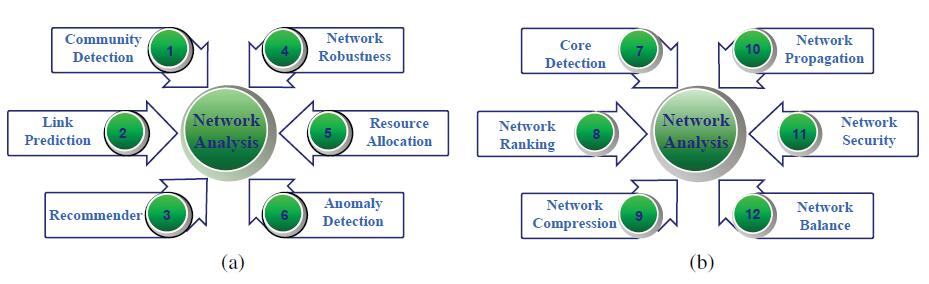 图二
图二
著名的网络属性
由于网络的结构常常会影响其功能,因此在分析复杂网络的结构特性中做了大量研究工作。有很多值得注意的网络,如:小世界网络(small-world property)、无标度网络(scale-free network)、群落结构(community structure property)等。
图三展示了一些典型的网络结构。
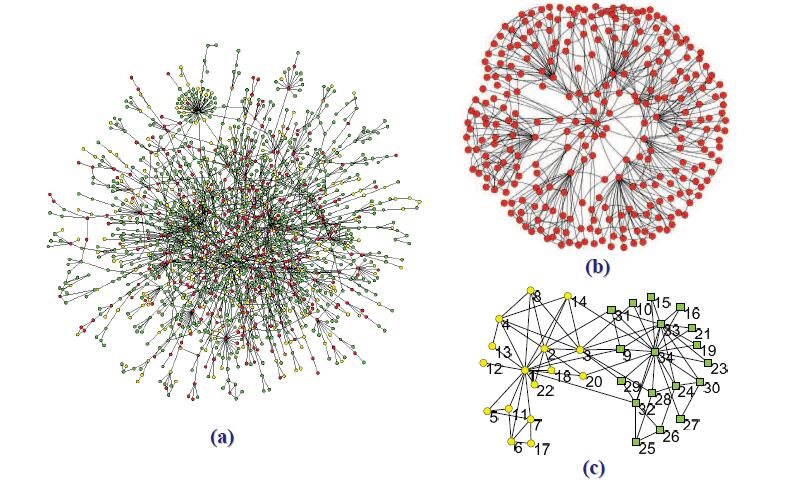 图三: (a) An example of a scale-free network. (b) An example of a small-world network.© An example of a network with two communities.
图三: (a) An example of a scale-free network. (b) An example of a small-world network.© An example of a network with two communities.
无标度网络在于其度分布没有一个特定的平均值指标,即大多数节点的度在此附近。在研究这个网络的度分布时,Barabási等人发现其遵守幂律分布(也称为帕累托分布),也就是说,随机抽取一个节点,它的度d是自然数k的概率:
$P(k) \sim {k^{ - \gamma }}$
也就是说 d=k 的概率正比于 k的某个幂次(一般是负的,记为 $ {-\gamma }$ )。因此k越大,d=k 的概率就越低。然而这个概率随 k增大而下降的“速度”是比较缓慢的:在一般的随机网络中,下降的速度是指数性的,而在无尺度网络中只是以多项式类的速度下降。
在现实中许多大规模的无尺度网络中,度分布的 $ {\displaystyle \gamma } $值介于2与3之间。在对数坐标系中,度分布将会是一条斜率介于-2至-3之间的直线。
小世界网络是一种它们间大部分的点都互不相邻,但是大部分的点通过其他少数的点就可以将他们联系在一起。
网络中的社区结构指的是,一个网络可以被划分为多个不同大小的群落,一个网络中具有相似属性的节点大都来源于同一个较大的群落,而不同的群落则来源较少。
图的符号表示
一般来说图用G={V,E}来进行表示,其中V表示网络中的点,E表示边(点之间的相互关系)。图G可以表示为一个${A_{n \times n}}$的邻接矩阵,其中${a_{ij}}$可表示为
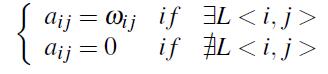 其中
其中L<i,j>表示节点i,j间的相互连接,${\omega _{ij}}$表示L<i,j>的权重。
如果他们有积极关系或者是消极关系,那么他们用分别用PE、和NE来表示
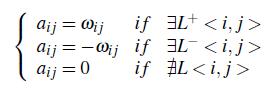
介绍非凸优化问题和计算计算
什么是优化问题
优化问题是一个非常活跃的讨论话题,在数学上可以简单的表示为:
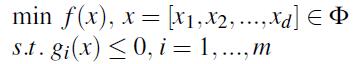 式(4)
x被称为决策向量,d是需要优化的参数个数,φ是在决策空间中的可行域,${g_i}(x)$是约束条件。
式(4)
x被称为决策向量,d是需要优化的参数个数,φ是在决策空间中的可行域,${g_i}(x)$是约束条件。
如果φ是凸集,f(x)可被称为凸函数,其中$\forall {x_1},{x_2} \in \phi ,\forall \alpha \in [0,1]$
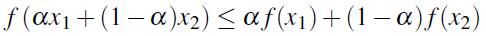
特别的,如果f(x)为严格凸函数,则
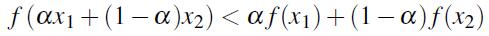
如果f(x)和${g_i}(x)$都是凸函数,那么我们可称为式(4)为凸优化问题。如果是严格凸优化问题,那么其只有一个最小值,且为全局最小值。但如果是非凸的,那么必然存在很多个局部或全局最小值。事实上,许多现实问题都是非凸优化问题。
同时,许多优化问题可以看做是多目标优化,他们超过一个目标函数f(x)需要优化,在数学上,多目标优化问题可以被描述为:
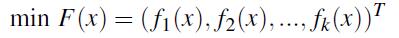 在这个多目标优化问题中,各个目标常常会出现冲突,比如一个目标的改进会导致另一个目标变差。因此得到一个能够使各个目标都达到最优的解是不存在的。在多目标优化中,我们常常做了一个妥协,我们把这类解称为帕累托最优(Pareto optimal solutions),下面有几个定义:
在这个多目标优化问题中,各个目标常常会出现冲突,比如一个目标的改进会导致另一个目标变差。因此得到一个能够使各个目标都达到最优的解是不存在的。在多目标优化中,我们常常做了一个妥协,我们把这类解称为帕累托最优(Pareto optimal solutions),下面有几个定义:
定义1 帕累托最优(Pareto Optimality)
定义2 帕累托占有(Pareto Dominance)
定义3 帕累托最优集合(Pareto Optimal Set)
定义4 帕累托前沿(Pareto Front)
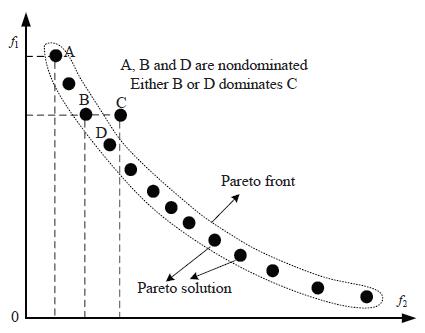
Figure 4: Graphical illustration of Pareto optimal solution and Pareto front.