在一般的机器学习任务中,已经有很多的数据预处理方法。本文要介绍的数据预处理方法是针对聚类算法。
在聚类中,通常将样本的所有特征数据组合成一个数值,然后计算两个样本之间的相似性。组合数据要求不同的特征具有相同的量纲。本文将讨论如何规范化、转换和创建分位数(normalizing, transforming, and creating quantiles),并讨论为什么分位数是转换任何数据分布的最佳默认选择。有了默认选项,就可以在不检查数据分布的情况下转换数据。
规范化数据 Normalizing Data
通过规范化数据,可以将多种特征转换为相同的量纲。特别是,规范化(normalizing)非常适合处理最常见的数据分布,即高斯分布。与分位数相比,规范化对数据量的要求更低。通过计算z-score对数据进行规范化,如下所示:
$$\begin{array}{*{20}{c}} {x' = (x - \mu )/\sigma } \\ {\mu = {\text{mean}}} \\ {\sigma = {\text{standard deviation}}} \end{array}$$让我们看看数据在标准化前后相似性变化的例子。在图1中发现红色与蓝色更相似,而不是黄色。这是因为,x轴和y轴上他们数据特征的量纲不同。因此,直接观察到的相似性可能是未经缩放的。使用z-score进行规范化后,所有特征具有相同的尺度。这时你会发现红色实际上更像黄色。因此,在对数据进行规范化之后,可以更准确地计算相似性。

图1:规范化前后的特征数据比较。
综上所述,当数据有如下之一情况时,推荐使用规范化:
- 数据服从高斯分布
- 缺少足够的数据来创建分位数
Log转换
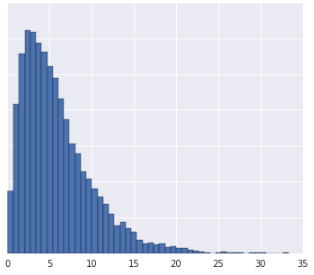
当数据分布表现为长尾分布时,如图所示,红点看起来与黄点更加相似。
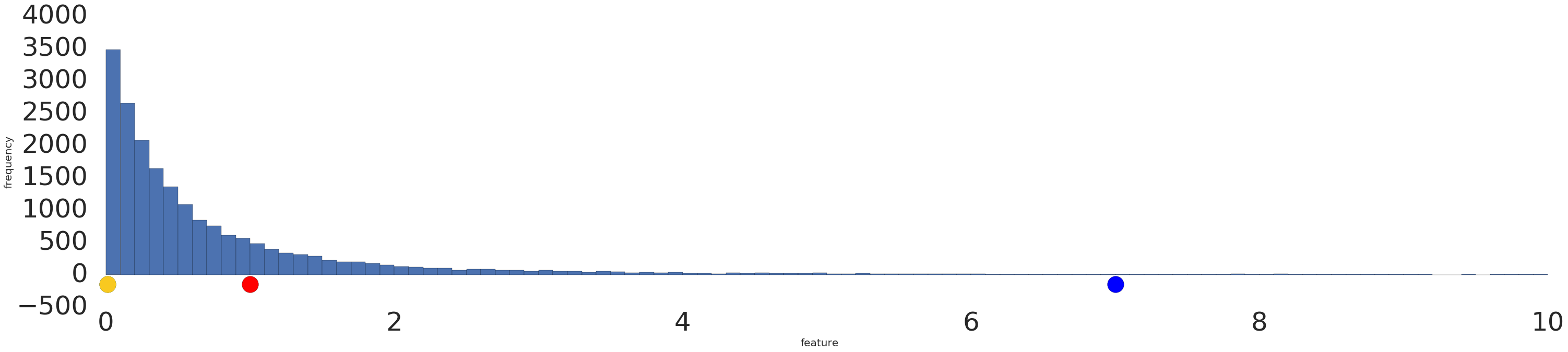
图2:幂率分布
我们对图2幂率分布的数据应用log转换,让数据分布变得更加平滑。结果如图3所示,红色目前与蓝色更相似。

图3:变化后的正态分布
分位数
规范化和log转换依赖于特定的数据分布。如果数据不符合高斯分布或幂律分布怎么办,是否有适用于任何分布的数据预处理方法。
尝试对如下分布进行预处理

图4:无法归类的数据分布
直观地说,如果两个样本之间只有少数几个样本,那么无论它们的值如何,这两个样本是相似的。相反,如果这两个样本之间有很多个其他样本,那么这两个样本就不那么相似了。因此,两个样本之间的相似性随着样本间的样本数量的增加而减少。
如果对数据进行规范化(normalizing)只会复制数据分布,因为规范化是一个线性变换。应用log转换也不能反映相似性的原理,如图5所示。
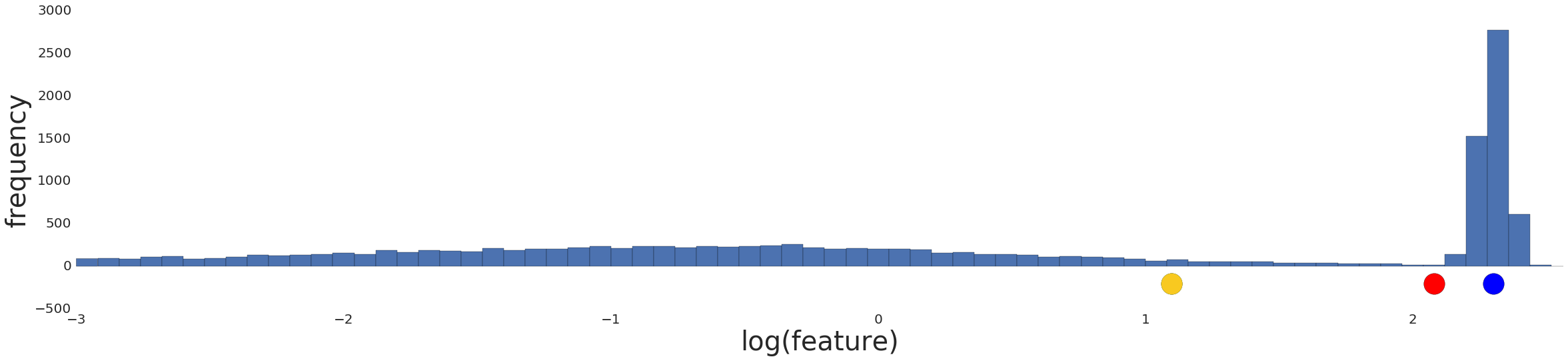
图5:对数据分布进行log转换
将数据划分为不同的区间,每个区间包含相同数量的样本。这些区间的边界称为分位数。
执行以下步骤将数据转换为分位数:
- 确定间隔的数量。
- 定义区间,使每个区间具有相同数量的样本。
- 用样本所在区间的索引替代原先的样本值。
- 将索引值缩放到[0,1],使索引与其他特征的数据范围相同。
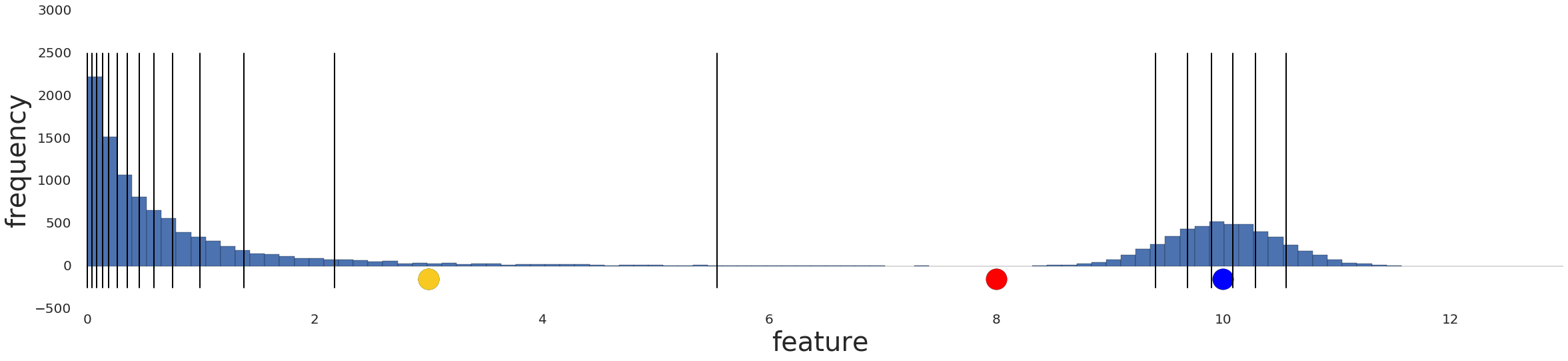
图6:使用分位数转换后的数据分布
将数据转换为分位数后,两个样本之间的相似性与这两个样本之间的样本数量成反比。在数学上,x是数据集中的任意一个样本:
$$sim(A,B) \approx 1 - |{\text{prob}}[x > A] - {\text{prob}}[x > B]|$$ $$sim(A,B) \approx 1 - |{\text{quantile}}(A) - {\text{quantile}}(B)|$$分位数是转换数据的最佳默认选择。然而,要建立可靠的底层数据分布的分位数指标,需要大量数据支撑。以经验来说,要建立$n$个分位数指标,至少需要$10n$个样本。如果没有足够的数据,请仍旧使用标准化(normalization)。
注意:
对于如下数据分布,应当使用分位数处理,因为它不属于幂率分布,也不属于某个标准的数据分布形式