南山小马

南山小马

0%

排序算法总结

发表于 更新于 分类于 Disqus：

刷完了剑指Offer，回过头再看看数据结构与算法。

选择排序

插入排序

把插入排序想象成，扑克牌中的洗牌，一张一张的来，把每一张未排序的牌插入到已经排好序的扑克牌中。

1
2
3
4
5
6
7
8
9
10
public void InsertSort(int[] arr) {
    if (arr == null || arr.length == 0) {
        return;
    }
    for (int i = 1; i < arr.length; i++) {
        for (int j = i; j > 0 && arr[j] < arr[j - 1]; j--) {
            exch(arr, j, j-1);
        }
    }
}

插入排序的哨兵 在插入排序的实现中，先找出最小的元素并将其置于数组的最左边，这样就能去掉内循环的判断条件 $j>0$。
这是一种常见的规避边界测试的方法，能够省略判断条件的元素通常被称为哨兵。

希尔排序

他也是一种属于插入排序类的方法，但在时间效率上比其他插入排序有较大改进。
直接插入排序的时间复杂度为$O({n^2})$，但是，若待排序序列为“正序”时，直接插入排序的时间复杂度为$O(n)$

基本思想：
先将整个待排序记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public void shellSort(int[] arr) {
    if (arr == null || arr.length == 0) {
        return;
    }
    int h = 1;
    while (h < arr.length / 3) {
        h = 3 * h + 1;
    }
    while (h >= 1) {
        // 将数组变成h有序
        for (int i = h; i < arr.length; i++) {
            // 注意 j >= h
            for (int j = i; j >= h && arr[j] < arr[j - h]; j -= h) {
                exch(arr, j, j - h);
            }
        }
        h /= 3;
    }
    return;
}

归并排序

把两个有序的数组归并成一个更大的有序数组。
要将一个数组排序，可以先（递归地）将它分成两半部分分别排序，然后将结果归并起来。
它能保证将任意长度为N的数组排序所需时间和NlogN成正比，但是它需要额外空间和N成正比。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public void mergingSort(int[] arr) {
    aux = new int[arr.length];
    mergingSortCore(arr, 0, arr.length - 1);
    return;
}

private void mergingSortCore(int[] arr, int lo, int hi) {
    if (lo >= hi) {
        return;
    }
    int mid = lo + (hi - lo) / 2;
    mergingSortCore(arr, lo, mid);
    mergingSortCore(arr, mid + 1, hi);
    merge(arr, lo, mid, hi);
}

private void merge(int[] arr, int lo, int mid, int hi) {
    int i = lo;
    int j = mid + 1;

    for (int k = lo; k <= hi; k++) {
        aux[k] = arr[k];
    }

    for (int k = lo; k <= hi; k++) {
        if (i > mid) {
            // 左半边完了，把右半边复制过来
            arr[k] = aux[j++];
        } else if (j > hi) {
            // 右半边完了，把左半边复制过来
            arr[k] = aux[i++];
        } else if (aux[i] > aux[j]) {
            // 左半边大于右半边，把右半边复制过来
            arr[k] = aux[j++];
        } else {
            // 右半边大于左半边，把左半边复制过来
            arr[k] = aux[i++];
        }
    }
}

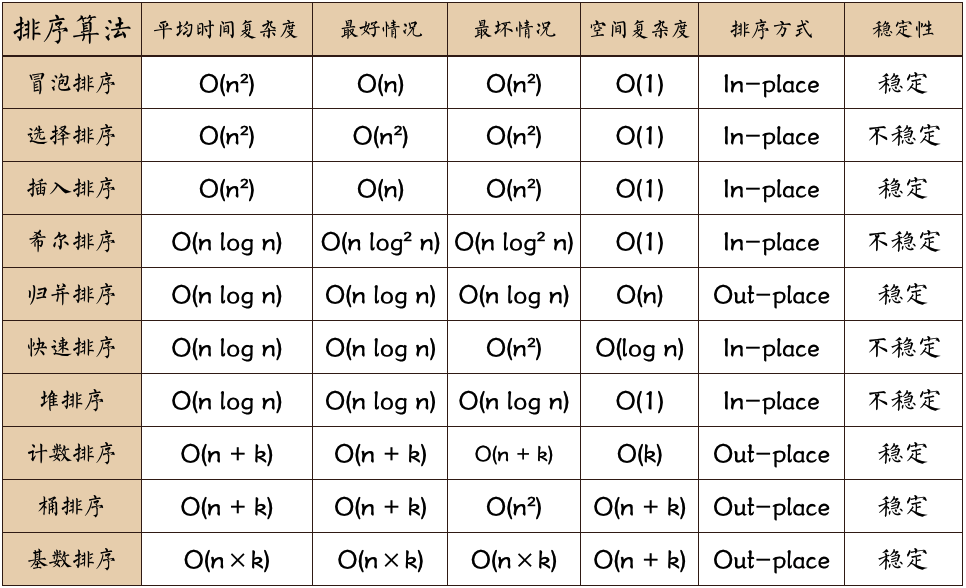
总结

sortpic